How to calculate worker compensation for Amazon Mechanical Turk
tl;dr: When calculating the average time it takes to complete a HIT, it may be more appropriate to use the geometric mean or the median instead of the arithmetic mean. You may otherwise spend considerably more money than necessary (in our case 50% more).
We usually try to set the reward for a HIT such that participants earn $6 per hour on average, which last time we checked was the recommended amount for academic research studies on Mechanical Turk. (Update: More recently the consensus seems to be that turkers should be payed at least the federal minimum wage, which is $7.25 at the time of writing.) However, some participants take an unusually long time to complete assignments (perhaps they were interrupted?) and that has unintended consequences for the calculation of the compensation payed to workers. Effectively, these participants make it appear as if we were paying less per hour than we actually do. Below I will shed some light on this issue using data from a recent study run by our lab.
Overall, 1122 workers participated in the experiment and each worker participated only once. The task was simple: Participants had to read a short passage of text (three sentences) and answer two easy questions about that passage. This was followed by a demographics questionnaire with nine items most of which were simple yes/no questions (“Are you a citizen of the United States?”). The whole thing could be finished in two to four minutes. However, we set the maximum time for submission to 60 minutes so that workers wouldn’t feel rushed.
The average completion time as shown by MTurk was 3 minutes and 46 seconds, not too far off from what we would expect for this task. But let’s have a closer look at the completion times:
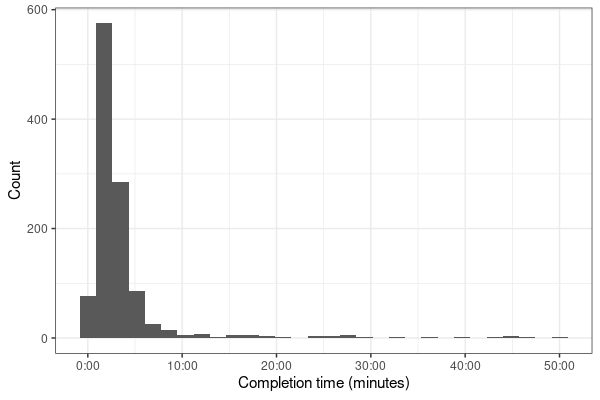
The plot shows how completion times are distributed in the data set. We see that the vast majority of workers finished in under eight minutes. However, there was also a smaller number of workers (about 6.5%) who took considerably longer, up to 50 minutes. For these participants the payment per hour is of course very low, but that’s not because we offered too little money, it’s because these participants did something else during that time.
To show the effect of these very slow workers, we calculate the average completion time again but this time only for workers who needed less than 8 minutes to finish. Given how simple the task was, eight minutes should easily be enough. The average time for workers who took less than 8 minutes was 2 minutes and 33 seconds. That’s 1 minute and 13 seconds faster than what we’ve got when we included very slow workers. This may not seem like a big difference, but it means that normal workers took only 68% of the time that we calculated based on the complete set of workers. A consequence is that normal workers actually made $9 per hour instead of the $6 we were aiming for. (Whether $6 or $9 per hour are appropriate is an independent question. Here we focus on the calculation of compensation.)
These numbers suggest that the average completion time across all participants as shown in the MTurk interface is actually misleading. One fix for that is to base the calculation of the compensation not on the arithmetic mean of the completion times but on the geometric mean. The geometric mean is often more appropriate when the scale has a lower bound as is the case with completion times.¹ Effectively, the geometric mean deemphasizes outliers and gives us an average completion time that is more representative of normal workers. In the present case, the geometric mean across all workers is 2 minutes and 21 seconds, which seems reasonable based on the numbers we've seen above: 2:21 is right were the peak is in the plot above. An alternative to the geometric mean is to use the median of the completion times, which is 2:20 in the present case.²
One caveat: Whether the geometric mean or the arithmetic mean is more appropriate depends on whether or not there are outliers. If the maximal time for submission is low, there can't be any extremely long completion times because those assignments would simply time out and not show up in the record. In that case, the arithmetic mean may be more appropriate. However, it's not advisable to set the maximal submission time too low because that may prevent some workers from submitting their results and getting compensated.
Footnotes:
- For the present purpose, the best way to think about the geometric mean is as the arithmetic mean of the logarithmized completion times back-transformed to the original time scale. In R, we would calculate
exp(mean(log(x))). - The median is a value that is bigger than the lower half of the values and smaller than the bigger half.